Pleasant Paradoxes : A compilation
A paradox is a seemingly absurd or contradictory statement or proposition which when investigated may prove to be well founded or true..This is a set of philosophical problems that contrary to the evidence of one's senses, the belief in infinity and change is mistaken, and in particular that progress is nothing but an illusion.
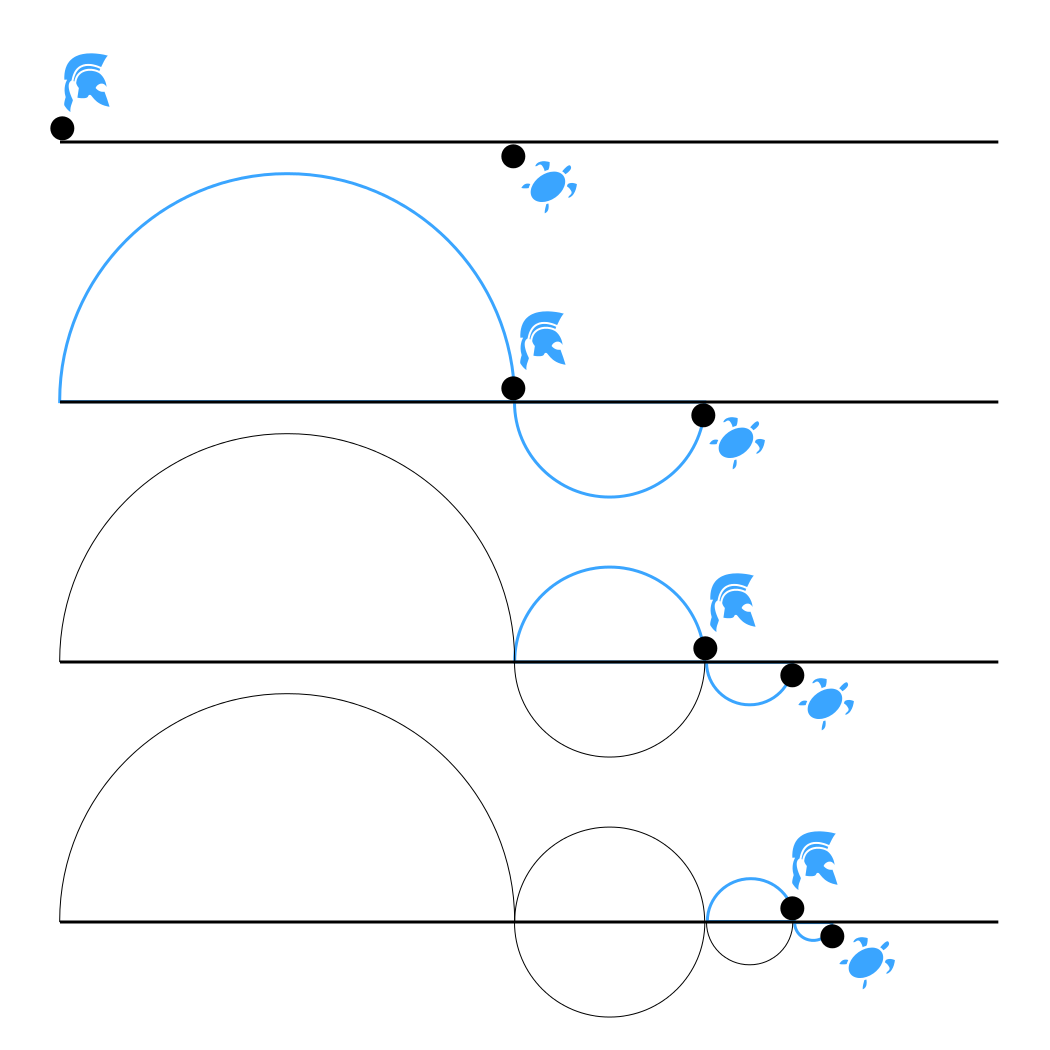
Achilles and the tortoise
In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead.
— as recounted by Aristotle, Physics VI:9, 239b15
In this paradox of Achilles and the tortoise, Achilles is in a footrace with the tortoise. Achilles allows the tortoise a head start
of 100 meters, for example. Supposing that each racer starts running at
some constant speed (one very fast and one very slow), then after some
finite time,
Achilles will have run 100 meters, bringing him to the tortoise's
starting point. During this time, the tortoise has run a much shorter
distance, say, 10 meters. It will then take Achilles some further time
to run that distance, by which time the tortoise will have advanced
farther; and then more time still to reach this third point, while the
tortoise moves ahead. Thus, whenever Achilles arrives somewhere the
tortoise has been, he still has some distance to go before he can even
reach the tortoise.
Dichotomy paradox
That which is in locomotion must arrive at the half-way stage before it arrives at the goal.
— as recounted by Aristotle, Physics VI:9, 239b10
This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility. This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite)
first distance could be divided in half, and hence would not be first
after all. Hence, the trip cannot even begin. The paradoxical conclusion
then would be that travel over any finite distance can neither be
completed nor begun, and so all motion must be an illusion. An alternative conclusion, proposed by Henri Bergson, is that motion (time and distance) is not actually divisible.This argument is called the Dichotomy because it involves repeatedly splitting a distance into two parts. It contains some of the same elements as the Achilles and the Tortoise paradox, but with a more apparent conclusion of motionlessness. It is also known as the Race Course paradox. Some, like Aristotle, regard the Dichotomy as really just another version of Achilles and the Tortoise.
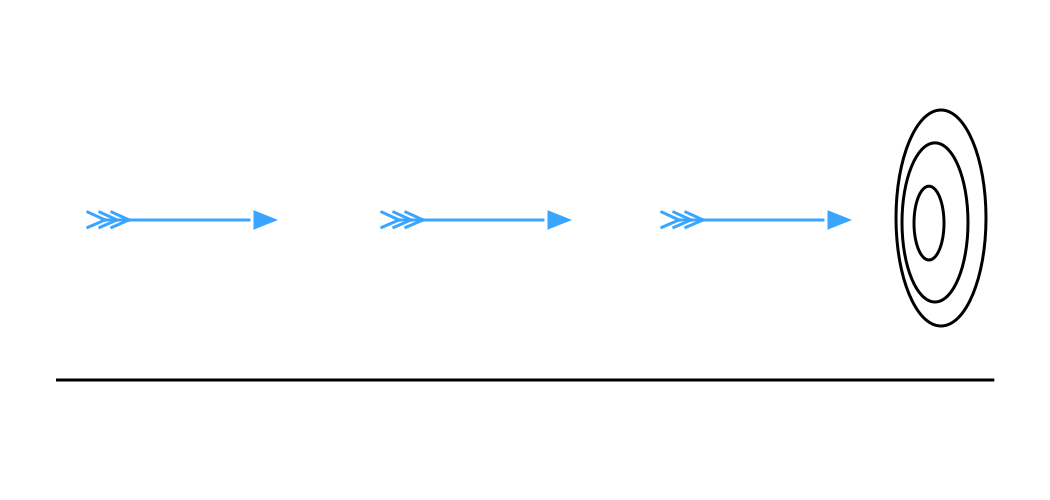
Arrow paradox
If everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless.
— as recounted by Aristotle, Physics VI:9, 239b5
In the arrow paradox, Zeno states that for motion to occur, an object
must change the position which it occupies. He gives an example of an
arrow in flight. He states that in any one (duration-less) instant of
time, the arrow is neither moving to where it is, nor to where it is
not.
It cannot move to where it is not, because no time elapses for it to
move there; it cannot move to where it is, because it is already there.
In other words, at every instant of time there is no motion occurring.
If everything is motionless at every instant, and time is entirely
composed of instants, then motion is impossible.
Whereas the first two paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.
The paradoxes in modern times
Infinite processes remained theoretically troublesome in mathematics until the late 19th century. The epsilon-delta version of Weierstrass and Cauchy developed a rigorous formulation of the logic and calculus involved. These works resolved the mathematics involving infinite processes. While mathematics can calculate where and when the moving Achilles will overtake the Tortoise of Zeno's paradox, philosophers such as Kevin Brown and Moorcroft claim that mathematics does not address the central point in Zeno's argument, and that solving the mathematical issues does not solve every issue the paradoxes raise.Popular literature often misrepresents Zeno's arguments. For example, Zeno is often said to have argued that the sum of an infinite number of terms must itself be infinite–with the result that not only the time, but also the distance to be travelled, become infinite. A humorous take is offered by Tom Stoppard in his play Jumpers (1972), in which the principal protagonist, the philosophy professor George Moore, suggests that according to Zeno’s paradox, Saint Sebastian, a 3rd Century Christian saint supposedly martyred by being shot with arrows, died of fright. However, none of the original ancient sources has Zeno discussing the sum of any infinite series. Simplicius has Zeno saying "it is impossible to traverse an infinite number of things in a finite time". This presents Zeno's problem not with finding the sum, but rather with finishing a task with an infinite number of steps: how can one ever get from A to B, if an infinite number of (non-instantaneous) events can be identified that need to precede the arrival at B, and one cannot reach even the beginning of a "last event"?
Some mathematicians and historians, such as Carl Boyer, hold that Zeno's paradoxes are simply mathematical problems, for which modern calculus provides a mathematical solution.
Some philosophers, however, say that Zeno's paradoxes and their variations (see Thomson's lamp) remain relevant metaphysical problems.
Quantum Zeno effect
The quantum Zeno effect (also known as the Turing paradox) is one of my favourites. It allows a particle's time evolution to be arrested by measuring it frequently enough with respect to some chosen measurement setting. Keeping the technical jargon aside, it can be said as, "a system can't change while you are watching it".
Comments
Post a Comment
Let us know what you think about it here...